Nu har så delkurs nummer två startat. Det handlar om vetenskaplig metod och kommer att vara fylld av vetenskapshistoria, som jag nu gillar sedan jag läste Russels kalkon (ska skriva en recension av den så fort jag hinner ;), och statistik, som jag sannolikt kommer att gilla stort eftersom det är siffror och siffror. Jag har ju också redan recenserat en bok i ämnet, Sant eller Sannolikt av Allan Gut, och den var grym!
Se anteckningar från föreläsning #1 som Sven höll 8 november 2008.
Efter avslutad kurs förväntas vi klara av att kunna genomföra en kvantitativ empirisk undersökning och använda insamlade data för att skriva en vetenskaplig rapport, samt att kunna beskriva och analysera sociala fenomen med lämpliga deskriptiva och bivariata metoder. Klockrent :)
Målet med kursen är att beskriva forskningsprocessen med tonvikt på problemformulering, hypotesprövning, urval, insamling, behandling och analys av data. Dessutom introduceras olika vetenskapsteoretiska problem inom olika vetenskapstraditioner. Innehållet kretsar kring: forskningsprocessens olika delar, vetenskapsteori, kvalitativ och kvantitativ metod, grundläggande statistik, genomförande av en kvantitativ undersökning, från problemformulering till avrapportering samt opposition.
Vi kommer att läsa ett antal böcker under delkursen. Får se om jag recenserar någon av dem. Vetenskapsteori för nybörjare ligger bra till för den verkar riktigt skoj ;)
De böcker vi ska läsa är:
– Backman, Jarl., Rapporter och uppsatser., Lund, Studentlitteratur, Senaste upplagan
– Bryman, Allan., Samhällsvetenskapliga metoder, Malmö, Liber, 2002
– Djurfeldt, Göran, Larsson, Rolf. & Stjärnhagen, Ola., Statistisk verktygslåda., Lund, Studentlitteratur, 2003
– Thurén, Torsten., Vetenskapsteori för nybörjare., Stockholm, Liber, 1996
Examination 1
Besvara följande:
1. Förklara innebörden av termerna validitet och reliabilitet. Ta gärna hjälp av egna exempel (2p).
2. Förklara skillnaden mellan kvantitativ och kvalitativ forskning med utgångspunkt i begreppen objektivism och konstruktivism (3p).
3. Förklara med egna exempel vad som kännetecknar en deduktiv respektive induktiv slutledning (3p).
4. Ge två exempel på frågor som Du som forskare måste ta hänsyn till för att Din forskning ska kunna anses uppfylla kraven på god forskningsetik (2p).
Svarets omfattning: ca 500 ord (+/- 75 ord). (Times New Roman 12p, 1,5 radavstånd, märk ditt svar med namn och numret på uppgiften)
Observera! Poängen på denna uppgift räknas samman och ingår i det slutliga betyget. Inga betyg sätts på de enskilda examinationerna. För mer information om detta se Information/Betyg
Svar: (Ladda ner inlämnat dokument)
1. Thurén beskriver reliabilitet och validitet på ett väldigt bra sätt (Thurén,2008:26-27). Där framgår det att Reliabilitet innebär att en mätning är korrekt genomförd och att vi kan lita på materialet. Validitet innebär att vi verkligen undersökt det vi ville undersöka och inget annat. Det där känner jag igen från verkliga livet som att reliabilitet är att mäta på rätt sätt, medan validitet är att mäta rätt saker. Vi diskuterar ofta på jobbet om våra medarbetarundersökningar. Dels om de är rätt utförda och att sammanställningarna är rätt gjorda och att beräkningarna är rätt utförda, dvs reliabilitet. Men dessutom ställer vi oss ofta frågan om vi har mätt det som är viktigt. Till exempel om det sammanställda resultatet verkligen är en indikator på det önskade engagemanget hos personalen, dvs en fråga om validitet.
2. Objektivismen utgår från att sociala fenomen existerar oberoende av oss aktörer (Bryman,2007:30-31) där omgivningen är fast och formar oss deltagare. Det gör att vi kan få en bild av de sociala fenomenen genom att mäta och observera aktörerna och deras handingar. Vi bör få likartade utfall och kan dra slutsatser av dessa. Det går att objektivt beskriva verkligheten, så det finns en tydlig grogrund för en kvantitativ ansats. I en konstruktivistisk världsbild skapas omgivningen av aktörerna (Bryman,2007:31-33). Det innebär att verksamheter och kulturer kontinuerligt formas av aktörerna. Det innebär att vi är inne i en konstant förändring där relationer och sociala fenomen ständigt utvecklas till nya former, vilket innebär att vi får svårt att arbeta med kvantitativa metoder utan behöver använda oss av ett kvalitativt arbetssätt för att bättre förstå skeendet och fenomenen och hela dess utveckling.
3. En induktiv slutsats sker med ett antal observationer som grund. Vi har djupintervjuat nyanställda på jobbet efter några månader för att höra hur de uppfattat sin introduktion, hur de ser på sin roll och företaget just nu osv. Det har vi gått igenom och analyserat och dragit slutsatser utifrån. Ett induktivt arbetssätt, som ju också starkt förknippas med ett kvalitativt arbetssätt (Bryman,2007:23).
Den deduktiva slutsatsen bygger på att vi redan har en definierad teori som vi vill bekräfta med observationer. Förra året genomförde vi en kundundersökning utifrån uppfattningen att det fanns kritik hos våra kunder inom några tjänsteområden. Vi fick vår teori bekräftad med råge men samtidigt också indikationer på var vi skulle behöva sätta in kraft för att rätta till vår verksamhet. Ett induktivt arbetssätt som också visar kopplingen till kvantitativ observation (Bryman,2007:22).
4. Jag vill lyfta fram två frågor som känns viktig för mig. Thurén nämner ett antal frågor (Thurén,2008:171-173) där alla känns viktiga men där Vad vill jag veta? är central eftersom den styr mig in i ett sammanhang. Eftersom jag upplever mig själv som tvärvetenskaplig i mina förhållningssätt känns det viktigt att vara tydlig med forskningsområdet och avgränsningarna. Frågan Varför vill jag veta det? är viktig för att definiera syftet med min forskning. Den är värdestyrd och det är viktigt att svaret tydligt kommer fram i beskrivningen. Jag vill använda mina kunskaper på praktiskt arbete i mitt företags eller våra kunders verksamheter och då blir det angeläget att vara tydlig med syftet eftersom jag kommer att ha tydliga relationer med de jag forskar på.
Thurén Torsten (2008). Vetenskapsteori för nybörjare. Liber
Byman Alan (2007). Samhällsvetenskapliga metoder. Liber
Betyg: 9 poäng (av 10 möjliga). I svaret på fråga 4 angående etiska problem är det som om Du “missat mål” lite grann. Med Bryman, kapitel 22, hade Du kunnat utveckla svaret bättre. Annars, Bra!
Examination 2 – Datoruppgift 1
Ni har fått tillgång till ett färdigt datamaterial som redan är inlagt i SPSS. Datamaterialet är ett urval bland barn i tredje årskurs. Urvalsstorleken är 198 barn (fiktiva) plus två (dessa är ej inlagda ännu). De två barn som inte finns med i filen finns i två enkäter och de ska Ni själva föra in i datafilen. De data vi har uppgift över är:
- Månad.
- Kön.
- Vikt.
- Längd.
- Antal syskon.
- Typ av peng, dvs. Veckopeng eller månadspeng.
- Storlek på peng (här är det både vecko-och månadspeng).
- Vem som bäddade sängen då undersökningen genomfördes.
- Hur många länder som den respondenten har besökt.
- Hur stor månadspeng respondenten har (här har veckopeng räknats om till måndaspeng).
- Kön i text (pojke eller flicka)
- Bäddar i text (mamma, pappa osv)
- Typ av peng, veckopeng eller månadspeng, i text.
- Vägsträcka till skolan.
Det Ni ska börja med är att lägga till två barn som fattas i datasetet. Svaren från dessa två barn finns i enkäterna. När dessa svar är tillagda ska det totalt finnas 200 barn/svar i datasetet (eller samplet).
Uppgift 1
Bestäm Centralmåtten. för tre av variablerna (valfria).
Ge tolkningsexempel för samtliga variabler. Var noga med att beskriva vilken datanivå variabeln tillhör och använd rätt centralmått till rätt datanivå.
Uppgift 2
Beskriv två variabler med hjälp av histogram.
Ge tolkningsexempel för varje variabel.
Uppgift 3
Beskriv variabeln ‘länder’ med en tabell över frekvenser och relativa frekvenser Ge ett tolkningsexempel.
Svar: (Ladda ner inlämnat dokument)
Uppgift 1
Vikt
Vikt är en variabel på kvotskalan. Det gör att vi kan räkna med aritmetiskt medelvärde (m) som centralmått (Djurefeldt, 2003:59). Medelvärdet är 35,85 kg. Det saknas värden för två observationer, vilket sannolikt påverkar medelvärdet, men inte i speciellt stor grad. Om vi fått två vikter på minimivärdet på 26 kg skulle vi ha fått ett medelvärde på 35,76. Med tanke på standardavvikelsen på 5,45 kg kan denna skillnad på 0,09 kg anses försumbar. Med två vikter på maxvärdet 49 kg skulle medelvärdet påverkas med 0,14 kg uppåt till 35,99. Samma tolkning här, i stort sett en försumbar påverkan.
Descriptive Statistics | |||||
N | Minimum | Maximum | Mean | Std. Deviation | |
| vikt i kg | 198 | 26 | 49 | 35,85 | 5,450 |
| Valid N (listwise) | 198 |
|
|
|
|
Med en kvotvariabel som vikt kan vi också använda median som centralmått (Djurfelt 2003:59) och med hjälp av SPSS finner vi att medianen är 35 kg. Den ligger nära det aritmetiska medelvärdet, vilket tyder på att medelvärdet visar ett rättvist värde.
Statistics | ||
| vikt i kg | ||
| N | Valid | 198 |
| Missing | 2 | |
| Median | 35,00 | |
| Percentiles | 25 | 32,00 |
| 50 | 35,00 | |
| 75 | 39,00 | |
Totalt antal kr per månad
Totalt antal kr per månad är en variabel på kvotskalan. Vi använder medelvärdet (m) som är 108,46 kr per månad. Det saknas värde för två observationer*, men medelvärdet skulle påverkas ganska lite, även av extremvärden.
Descriptive Statistics | |||||
N | Minimum | Maximum | Mean | Std. Deviation | |
| total antal kr per månad | 198 | 50 | 250 | 109,01 | 39,587 |
| Valid N (listwise) | 198 |
|
|
|
|
*I datafilen återfinns ett värde 0 men det är för en observation där vi saknar angivelse för både vecko- eller månadspeng och angiven summa per utbetalningstillfälle. Efter justering av 0-värdet till ett saknat värde får vi sammanställningen ovan.
Medianen för Totalt antal kr per månad är 100 kr och pekar på att medelvärdet är lite högt. Med en blick i histogrammet i uppgift 2 (se sidan 6) ser vi att det stämmer, och att det aritmetiska medelvärdet dras upp på grund av en mängd höga observationer, men att de flesta fördelar sig kring medianvärdet.
Statistics | ||
| total antal kr per månad | ||
| N | Valid | 198 |
| Missing | 2 | |
| Median | 100,00 | |
| Percentiles | 25 | 80,00 |
| 50 | 100,00 | |
| 75 | 130,00 | |
Vem som bäddar sängen
Vem som bäddar sängen är en nominalvariabel. Det går endast att använda typvärde som centralmått (Djurfeldt,2003:47). Typvärdet är mamma som bäddar sängen 70 gånger av de observerade 198 gångerna. Det saknas värde för två observationer, men de påverkar inte typvärdet alls. Anmärkningsvärt är att pappa förekommer färre gånger än själv, vilket jag i min egen roll som pappa finner både lustigt och skrämmande.
vem som bäddar sängen | |||||
Frequency | Percent | Valid Percent | Cumulative Percent | ||
| Valid | Själv | 60 | 30,0 | 30,3 | 30,3 |
| Mamma | 70 | 35,0 | 35,4 | 65,7 | |
| Pappa | 58 | 29,0 | 29,3 | 94,9 | |
| Ingen | 10 | 5,0 | 5,1 | 100,0 | |
| Total | 198 | 99,0 | 100,0 |
| |
| Missing | System | 2 | 1,0 |
|
|
| Total | 200 | 100,0 |
|
| |
Uppgift 2
Födelsemånad
Födelsemånad är en variabel på ordinalskalan men som har en sådan struktur att ett centralmått som median har svårt att ge någon information alls om mätningen. Typvärdet är såklart intressant när det gäller en tidsorienterad mätning. Bland alla månader är maj i detta exempel med 29 av 199 observationer, eller 14,6% av alla angivna födelsemånader den vanligaste födelsemånaden.
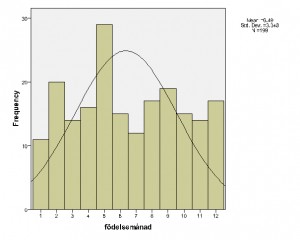
Histogram
Men mer intressant i fallet med födelsemånad är hur utfallet fördelar sig över året. Det är exakt tolv olika värden som variabeln kan ikläda sig och de är dessutom väldigt lätta att förstå intuitivt, årets månader lär vi ju oss tidigt som barn.
Av histogrammet ser vi att födelsemånaderna är någorlunda jämnt fördelade över året. Vi har dock tre månader som sticker ut ur mätningen; januari, maj och juli.
Maj står för en stor andel medan januari och juli för en ovanligt liten del av alla födslar vilka med det sunda förnuftet borde vara jämnt fördelade över året. Om vi kikar på frekvensfördelningen ser vi mer i detalj hur utfallet fördelar sig.
födelsemånad | |||||
Frequency | Percent | Valid Percent | Cumulative Percent | ||
| Valid | Januari | 11 | 5,5 | 5,5 | 5,5 |
| Februari | 20 | 10,0 | 10,1 | 15,6 | |
| Mars | 14 | 7,0 | 7,0 | 22,6 | |
| April | 16 | 8,0 | 8,0 | 30,7 | |
| Maj | 29 | 14,5 | 14,6 | 45,2 | |
| Juni | 15 | 7,5 | 7,5 | 52,8 | |
| Juli | 12 | 6,0 | 6,0 | 58,8 | |
| Augusti | 17 | 8,5 | 8,5 | 67,3 | |
| September | 19 | 9,5 | 9,5 | 76,9 | |
| Oktober | 15 | 7,5 | 7,5 | 84,4 | |
| November | 14 | 7,0 | 7,0 | 91,5 | |
| December | 17 | 8,5 | 8,5 | 100,0 | |
| Total | 199 | 99,5 | 100,0 |
| |
| Missing | System | 1 | ,5 |
|
|
| Total | 200 | 100,0 |
|
| |
Då ser vi att Maj har 14,6% av alla giltiga värden för födelsemånad. Det sunda förnuftet säger att ett normalutfall borde ligga kring 8,25% för alla månader. Nu är det säkert inte helt jämnt fördelat, men det är nog viktigt att kontrollera sannolikheten i detta utfall. På samma sätt är Januari med 5,5% och juli med 6,0% av alla barn i underkant och bör ställas under en extra analys av utfallet.
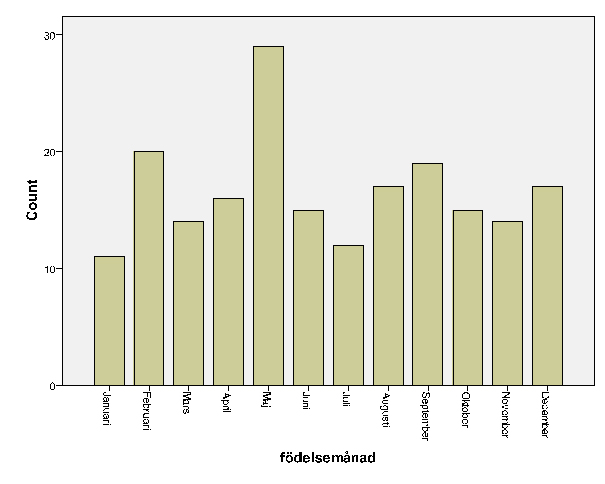
Stapeldiagram
Med tanke på att födelsemånad är en ordinalskalevariabel är histogram ett något missvisande sätt att beskriva materialet. Ett stolpdiagram (Djurfeldt,2003:51), som tydligare visar att variabeln har ett antal diskreta värden att anta, är mer rättvist. Det visar SPSS också genom att automatiskt presentera varje stolpe med månadsnamnet.
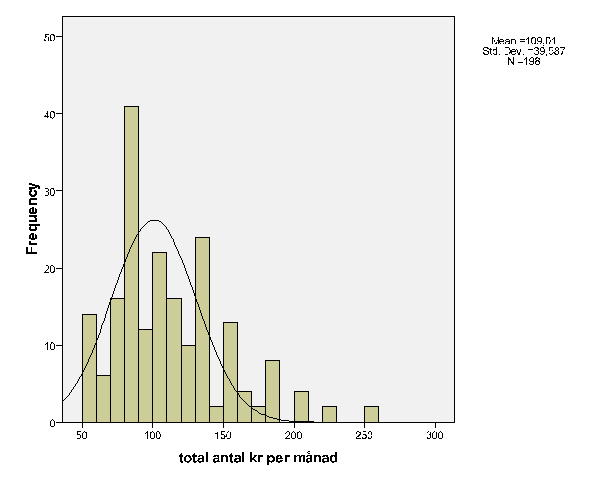
Totalt antal kr per månad
Totalt antal kr per månad är en variabel på kvotskalan och passar bra att visa med histogram. Vi ser att den stora mängden observationer återfinns kring medianen som är 100 kr vilket analysen i uppgift 1 visar (se sidan 3). Histogrammet visar tydligt hur förskjuten fördelningen är mellan olika månadspengar. Det är några värden som sticker iväg och frågan är hur giltiga de allra högsta observationerna är. Finns det andra behov som styrt registreringen av värden över 200 kronor, eller finns det brister i omformningen av veckopeng till månadspeng? Det är frågor som väcks när histogrammet studeras.
Uppgift 3
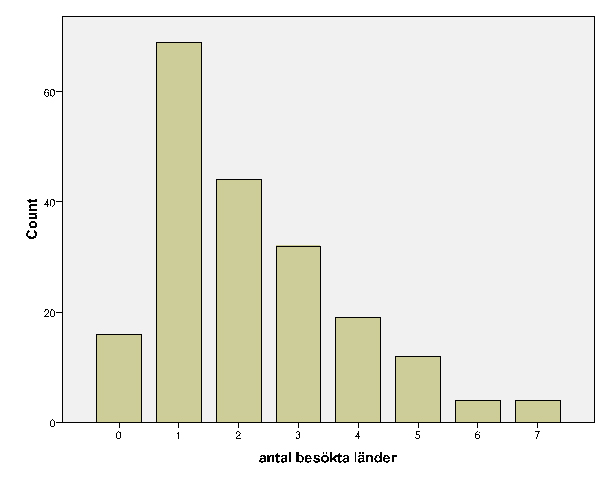
Variabeln Antal besökta länder har inget bortfall så vi har alltså 200 mätvärden. De fördelar sig från 0 besökta länder till 7 besökta länder. Fördelningen är ojämn. Variabeln hör till kvotskalan men ändå är typvärdet ett av de starkaste måtten i en snabb analys.
antal besökta länder | |||
Frequency | Percent | ||
| Valid | 0 | 16 | 8,0 |
| 1 | 69 | 34,5 | |
| 2 | 44 | 22,0 | |
| 3 | 32 | 16,0 | |
| 4 | 19 | 9,5 | |
| 5 | 12 | 6,0 | |
| 6 | 4 | 2,0 | |
| 7 | 4 | 2,0 | |
| Total | 200 | 100,0 | |
Centralmått
Typvärdet, dvs”1 resa” har modalvärdet 34,5% av alla observationer vilket är mer än 1 av 3. Om vi gör en grov förenkling av vår modell och låter resultatet beskrivas genom värdena 0 aldrig, 1-2 resor, 3 resor eller fler, ser vi att värdet 1-2 resor står för 56,5% av alla svar.
Kumulativ analys
Om vi gör en analys av den kumulativa fördelningen kan vi se ytterligare en rätt kraftig signal. Det visar sig att 92% av alla elever har någon gång besökt ett annat land.
antal besökta länder | |||||
Frequency | Percent | Valid Percent | Cumulative Percent | ||
| Valid | 7 | 4 | 2,0 | 2,0 | 2,0 |
| 6 | 4 | 2,0 | 2,0 | 4,0 | |
| 5 | 12 | 6,0 | 6,0 | 10,0 | |
| 4 | 19 | 9,5 | 9,5 | 19,5 | |
| 3 | 32 | 16,0 | 16,0 | 35,5 | |
| 2 | 44 | 22,0 | 22,0 | 57,5 | |
| 1 | 69 | 34,5 | 34,5 | 92,0 | |
| 0 | 16 | 8,0 | 8,0 | 100,0 | |
| Total | 200 | 100,0 | 100,0 |
| |
Det är vid en första anblick en väldigt hög siffra, och nästan var femte barn har varit i fyra eller fler länder. Vi kan fortsätta och se på spridningen av länderna.
Vi ser det vi redan visste, att 1 och 2 besök i andra länder dominerar. Spridningen upp till maxvärdet sker med färre och färre observationer. Om vi minns diagrammet över månadspeng (se histogram uppgift 1 på sidan 8) som liknar spridningen av resor till andra länder, väcks en hypotes om att variablerna har ett samband.
Djurfeldt Göran, Larsson Rolf, Stjärnhagen Ola (2003). Statistisk verktygslåda. Studentlitteratur
Betyg: 4 poäng (av 4 möjliga). Din inlämningsuppgift ser bra ut. Om jag ska vara riktigt petig så saknas en förklaring till begreppet relativa frekvenser i uppgift 3, men det verkar som om Du ändå har förstått vad det handlar om. Vad gäller författande av vetenskapliga rapporter med tabeller o liknande information så finns det några olika skolor. Din redovisning ser helt ok ut för en uppgift av den här typen. Om det hade varit en C-uppsats eller liknande hade det kanske varit aktuellt med ánnan kritik, vanligtvis brukar all information som hör till, eller så att säga tar avstamp i tabellen placeras under densamma. I Backman “rapporter och uppsatser” ges en bra sammanfattning av det viktigaste man bör tänka på, även om det kan vara ok. Om Du är intresserad av att se hur det brukar se ut i vanliga vetenskapliga rapporter av akademisk art tipsar jag Dig att blädra igenom någon vetenskaplig artikel, det är de som sätter standarden. En artikel som innehåller mycket av både diagram, tabeller och regressionanalyser är: Culture and Identity-Protective Cognition: Explaining the White-Male Effect in Risk Perception.
Om Du går in på Miun/biblioteket och går på “söka artiklar” kommer du att finna en länk till Google Scholar (betaltjänst, måste gå via biblioteket). Klistra in länken där så kommer Du att kunna klicka Dig fram till artikeln i fulltext PDF.
Examination 3 – Datoruppgift 2
Uppgift 1
Beräkna produktmomentkorrelationskoefficienten för sambandet mellan längd och
vikt. Ge en kortfattad tolkning.
Uppgift 2
I den här uppgiften skall vi undersöka ifall flickor och pojkar är lika långa och skiljer i vikt i årskurs 3. Detta skall ni göra med hjälp av signifikansprövning av medelvärdesskillnader av variablerna ‘längd’ och ‘vikt’.
Uppgift 3
Ytterligare en övningsfil innehåller (fiktiva) enkätsvar från 400 slumpvis utvalda personer i en kommun. Undersökningens bakgrund är att vi vill studera hur variabler som personers ålder, kön, utbildningsnivå och yrke påverkar sannolikheten att personer är arbetslösa.
I denna fil har vi följande variabler:
- Kön (1=kvinna 2=man)
- Position (1= arbetslös 2=har arbete)
- Ålder (1=äldre, 2= yngre)
- Utbildning ‘utbild’ (grundskola = 1, gymnasiet = 2, högskolan/universitet = 3, forskarutbildning = 4)
För att få en enkel modell att analysera kan man i ett sådant här fall vilja använda endast två koder för varje variabel. Koda om variabeln ‘utbildning’ så att en ny variabel ‘utb.kat’ bildas. Individerna med värden 3 eller 4 i ‘utbildning’ är högutbildade. Ge 1-2 etiketten lågutbildade och 3-4 etiketten högutbildade i ‘utb.kat’.
Uppgift 4
Vi använder oss av samma datafil som föregående uppgift (dvs. uppgift 6). Er uppgift är att genomföra ett Chi-två test. Ni skall undersöka om det föreligger någon signifikant skillnad mellan könen och position på arbetsmarknaden. Samt undersöka om det föreligger någon signifikant skillnad vad gäller utbildningskategori (hög/låg utbildning) och position på arbetsmarknaden. Ge tolkningsexempel på era resultat.
Svar: (Ladda ner inlämnat dokument)
Uppgift 1
Produktmomentkorrelationskoefficienten
Både Vikt och Längd är variabler på kvotskalan och således kvantitativa variabler. Det innebär att vi inte har så stor nytta av korstabeller om vi vill leta efter samband, allra helst eftersom värdena i de båda variablerna är kontinuerliga och med stor spridning, (Djurfeldt, 2003:161). Det gör att vi får använda andra sätt för att hitta eventuella korrelationer, och ett är att räkna ut produktmomentkorrelationskoefficienten r. I SPSS är det viktigt att veta att det vi är ute efter är Pearsons r eftersom det går att använda flera andra varianter. Pearsons r (Djurfeldt, 2003:161ff) beskriver hur mycket varje observations x- och y-variabler (Vikt och Längd i denna uppgift) varierar runt sina respektive medelvärden. Avsaknad av samband ger r=0 medan ett fullständigt samband ger r som närmar sig -1 eller +1.
Correlations | |||
längd i cm | vikt i kg | ||
| längd i cm | Pearson Correlation | 1 | ,702** |
| Sig. (2-tailed) |
| ,000 | |
| N | 200 | 198 | |
| vikt i kg | Pearson Correlation | ,702** | 1 |
| Sig. (2-tailed) | ,000 |
| |
| N | 198 | 198 | |
| **. Correlation is significant at the 0.01 level (2-tailed). | |||
Efter körning i SPSS visar det sig att korrelationenkorrelationskoefficienten r mellan längd och vikt är 0,702 vilket är ganska starkt, vilket vi kan förstå med det sunda förnuftet. Det innebär att spridningen för varje barns vikt och längd jämfört med dess respektive medelvärde följer varandra med r-värdet 0,702. Att det inte finns en fullständig koppling mellan längden och vikten, vilket skulle ha visats med ett r-värde på upp mot 1,0 förstår vi också med sunda förnuftet eftersom vi människor är väldigt olika byggda.
I materialet från SPSS kan vi också se att vi har en signifikans på 1% nivån vilket ger en stor sannolikhet att vi har ett sambanden enligt det beräknade värdet på r.
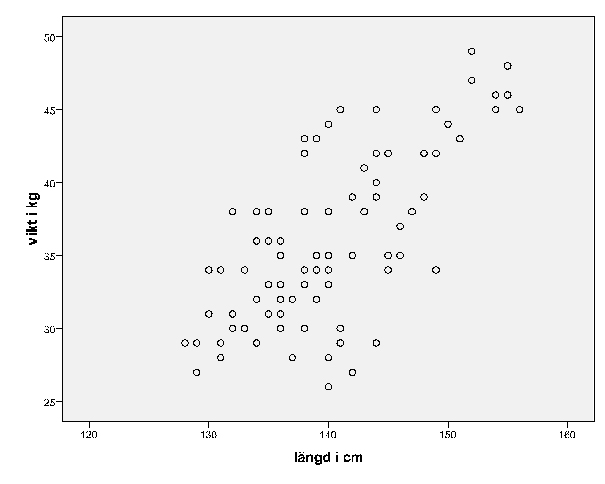
Hur spridningen rent grafiskt ser ut går att se med ett spridningsdiagram. Här kan vi med blotta ögat se att det finns en tydlig koppling, men att det finns ganska stora variationer mellan de olika värdena för längd respektive vikt.
Uppgift 2
Flickor och pojkar – vikt och längd
I den här uppgiften skall vi undersöka ifall flickor och pojkar är lika långa och skiljer i vikt i årskurs 3. Utifrån det underlag vi har kan vi testa medelvärdet för pojkar respektive flickor och se om vi kan dra någon slutsats om skillnader i vikt och längd samt bedöma om den skillnaden är statistiskt försvarbar. Det handlar om en bivariat analys med en kvalitativ x-variabel (Kön) och en kvantitativ y-variabel (Vikt respektive Längd) med hypotesprövning (Djurfeldt, 2003:241ff). Vi vill göra det med 95 % sannolikhet.
Vikt
Vi använder SPSS för att ta fram underlag för att testa våra värden. Vi börjar med vikt.
Group Statistics | |||||
| kön | N | Mean | Std. Deviation | Std. Error Mean | |
| vikt i kg | Pojke | 95 | 37,42 | 5,856 | ,601 |
| Flicka | 103 | 34,41 | 4,622 | ,455 | |
En medelvärdeskörning på variabeln vikt för flickor och pojkar ser vi att pojkar har mp=37,4 kg och för flickor mf=34,4. Det ser ut som en tydlig skillnad, men det är inte uppenbart att alla skillnader är statistiskt signifikanta och det är alltså det vi ska testa. Vi sätter våra hypoteser:
H0: mp = mf dvs. mp – mf = 0, ingen skillnad – flickor och pojkar väger lika mycket
H1: mp ≠ mf dvs. mp – mf ≠ 0, det finns en skillnad – flickor och pojkar väger olika
Independent Samples Test | ||||||||||
Levene’s Test for Equality of Variances | t-test for Equality of Means | |||||||||
|
| 95% Confidence Interval of the Difference | ||||||||
F | Sig. | t | df | Sig. (2-tailed) | Mean Difference | Std. Error Difference | Lower | Upper | ||
| vikt i kg | Equal variances assumed | 10,967 | ,001 | 4,035 | 196 | ,000 | 3,013 | ,747 | 1,540 | 4,486 |
| Equal variances not assumed |
|
| 3,997 | 178,690 | ,000 | 3,013 | ,754 | 1,526 | 4,501 | |
Med hjälp av SPSS får vi först en bedömning av variansskillnaden. SPSS använder Levenes test (Djurfeldt, 2003:244f) för att bedöma skillnaden i s2. Vi kan läsa av det uträknade F-värdet nedan, men enklast är att se Sig. som ger oss p-värdet direkt. Eftersom vi är ute efter en sannolikhet på 95% krävs det att p-värdet är högre än eller lika med 5%, dvs. p≥0,05. Det är det inte i det här fallet. Med Sig.=0,001 vet vi att skillnaden mellan flickornas och pojkarnas varianser är för stor, och vi måste avläsa den undre raden i SPSS-materialet.
Ur den undre raden läser vi av att t=3,997 med en hög nivå på frihetsgraden, df=178,69, vilken är lite lägre än den frihetsgrad vi haft med lika varianser, och utan att veta antar jag frankt att det har att göra med att vi har en stor differens mellan de båda urvalen och att vi har ett högre beviskrav för vårt framräknade t-värde än om varianserna varit lika. Med ett lägre df blir det kritiska t-värde som vi måste nå upp till för att kunna förkasta vår nollhypotes H0 högre. I vårt exempel kan vi direkt läsa av p-värdet i kolumn Sig. (2-tailed) där det blir uppenbart att vår nollhypotes inte håller. Med ett p-värde på 0,000 är det väldigt liten chans att vår H0 är rätt utan vi har en signifikant skillnad mellan vikt på pojkar och flickor.
Slutsatsen är att flickor och pojkar skiljer i vikt.
Längd
Group Statistics | |||||
| kön | N | Mean | Std. Deviation | Std. Error Mean | |
| längd i cm | pojke | 95 | 141,12 | 6,628 | ,680 |
| flicka | 105 | 138,63 | 5,848 | ,571 | |
När vi studerar längd så ser vi liknande skillnader i medelvärdet som i fallet med vikt. Med blotta ögat upplevs dock skillnaden som mindre än för vikten. För längd är mp=141,1cm och mf=138,6 vilket innebär en skillnad på endast 2,5 cm.
Vi vill nu testa om vår hypotes är korrekt och om skillnaden mellan pojkar och flickor är signifikant.
H0: mp = mf dvs. mp – mf = 0, ingen skillnad – flickor och pojkar är lika långa
H1: mp ≠ mf dvs. mp – mf ≠ 0, det finns en skillnad – flickor och pojkar är olika långa
Independent Samples Test | ||||||||||
Levene’s Test for Equality of Variances | t-test for Equality of Means | |||||||||
|
| 95% Confidence Interval of the Difference | ||||||||
F | Sig. | t | df | Sig. (2-tailed) | Mean Difference | Std. Error Difference | Lower | Upper | ||
| längd i cm | Equal variances assumed | 3,312 | ,070 | 2,819 | 198 | ,005 | 2,487 | ,882 | ,747 | 4,227 |
| Equal variances not assumed |
|
| 2,802 | 188,514 | ,006 | 2,487 | ,888 | ,736 | 4,238 | |
På samma sätt som för vikten gör vi först en bedömning av variansskillnaden. Levenes test ger F-värdet nedan, men vi kikar direkt på Sig. för att få p-värdet. Eftersom vi är ute efter en signifikans på 95% nivån krävs det att p-värdet är högre än eller lika med 5 %, dvs. p≥0,05. Det är det också. Vi har fått ett p=0,07 och då vet vi att skillnaden mellan flickornas och pojkarnas varianser håller för en uträkning av t-värdet genom att anta att s2 för pojkar respektive flickor är lika, så då kan vi läsa den övre raden i SPSS-materialet.
På den övre raden läser vi att t=2,819 med frihetsgraden df=198 (nf + np – 2). I exemplet kan vi direkt läsa av p-värdet i kolumn Sig. (2-tailed) där det visar sig att vår nollhypotes inte heller i fallet med längd håller. För att H0 ska hålla krävs ett p-värde på minst 5% eller 0,05. Vårt beräknade p-värde på 0,005 visar således att vi har en signifikant grund för att förkasta nollhypotesen och att vi har en till 95 % sannolikt signifikant skillnad mellan pojkar och flickors längder.
Slutsatsen är att flickor och pojkar inte är lika långa.
Uppgift 3
Genomförd. Inget att redovisa.
Uppgift 4
Korrelation mellan kön och position
I den här uppgiften skall vi, med en ny datafil, undersöka ifall det finns någon skillnad mellan de olika könen och deras respektive position på arbetsmarknaden. Vi ska också bedöma om den skillnaden är statistiskt försvarbar. På samma sätt ska vi undersöka skillnader mellan olika utbildningskategorier (hög/låg utbildning) och position på arbetsmarknaden
Vi vill göra det med 95 % sannolikhet.
Kön och Position på arbetsmarknaden
När vi har två kvalitativa variabler som vi vill undersöka kan vi använda korstabulering (Djurfeldt, 2003:148ff) och sambandsmått, som till exempel Chi2 (Djurfeldt, 2003:225ff). Som i exemplen ovan är det nollhypotes och mothypotes vi ställer upp först:
H0: Oberoende råder mellan variablerna, dvs. kön påverkar inte position på arbetsmarknaden.
H1: Beroende råder mellan variablerna, dvs. kön påverkar position på arbetsmarknaden.
kön * position på arbetsmarknaden Crosstabulation | ||||
| Count | ||||
position på arbetsmarknaden | Total | |||
Arbetslös | Har arbete | |||
| kön | Kvinna | 40 | 145 | 185 |
| Man | 28 | 187 | 215 | |
| Total | 68 | 332 | 400 | |
Chi2-test arbetar med korstabeller (Djurfeldt, 2003:225f) som vi kört fram via SPSS enligt tabellen ovan. Det är förhållandet mellan två kvalitativa variabler som vi vill analysera. Vi jämför de observerade frekvenserna (O), som listas i tabellen ovan, med den förväntade fördelning (E) som vi skulle ha fått vid ett slumpmässigt utfall. Det går till genom att vi räknar ut en förväntad frekvens för alla fyra frekvenser och räknar chi2 med formeln:
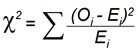
Och utifrån värdena ovan får vi den egna beräkningen som följer:
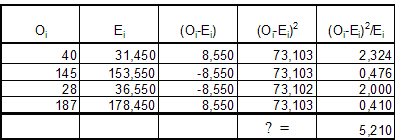
Detta är Pearsons Chi2 som är den vanligaste (Djurfeldt, 2003:225). Vi behöver nu testa detta Chi2-värde 5,210 mot det kritiska värdet för våra sannolikhetskrav med hänsyn till antalet frihetsgrader. Frihetsgraderna är (kolumner-1)*(rader-1) och blir i vårt fall 1. Om vi vill testa vår hypotes med en 95% sannolikhet läser vi av det kritiska Chi2-värdet i tabellen (Djurfeldt, 2003:494) kolumn P%=5 för Frihetsgrader=1. Där får vi 3,841 som kritiskt värde. Vi ligger långt över detta värde och kan alltså förkasta vår nollhypotes och att ett beroende råder mellan variablerna, dvs. kön påverkar position på arbetsmarknaden.
Chi-Square Tests | |||||
Value | df | Asymp. Sig. (2-sided) | Exact Sig. (2-sided) | Exact Sig. (1-sided) | |
| Pearson Chi-Square | 5,210a | 1 | ,022 |
|
|
| Continuity Correctionb | 4,619 | 1 | ,032 |
|
|
| Likelihood Ratio | 5,204 | 1 | ,023 |
|
|
| Fisher’s Exact Test |
|
|
| ,024 | ,016 |
| Linear-by-Linear Association | 5,197 | 1 | ,023 |
|
|
| N of Valid Cases | 400 |
|
|
|
|
| a. 0 cells (,0%) have expected count less than 5. The minimum expected count is 31,45. | |||||
| b. Computed only for a 2×2 table | |||||
Med SPSS kan vi göra samma körning och få ett Chi2-test genomfört på ett snabbare sätt. I tabellen ovan får vi olika beräkningar för Chi2 redovisade. Vi kan jämföra med beräkningen ovan och ser att vi har fått samma värde för Pearsons Chi2, nämligen 5,210. Där får vi också ett värde för sannolikheten på samma rad (Asymp. Sig. (2-sided)) som anges till 0,022, dvs. risken för att vi felaktigt skulle förkasta nollhypotesen är 2,2%. Vi ville ha en sannolikhet på minst 95 % för att det finns en skillnad mellan kön och position på arbetsmarknaden och det nådde vi.
Slutsatsen är att det föreligger en signifikant skillnad mellan könen och positionen på arbetsmarknaden.
Utbildningskategori och Position på arbetsmarknaden
Vår analys av skillnader mellan utbildningskategori och position på arbetsmarknaden följer samma mönster som i ovanstående redovisning. Det är genom en korstabell och med en Chi2-analys vi gör beräkningarna.
Som i exemplen ovan är det nollhypotes och mothypotes vi ställer upp först:
H0: Oberoende råder mellan variablerna, dvs. utbildningskategori påverkar inte position på arbetsmarknaden.
H1: Beroende råder mellan variablerna, dvs. utbildningskategori påverkar position på arbetsmarknaden.
utbildningskategori * position på arbetsmarknaden Crosstabulation | ||||
| Count | ||||
position på arbetsmarknaden | Total | |||
Arbetslös | Har arbete | |||
| utbildningskategori | Låg | 66 | 257 | 323 |
| Hög | 2 | 75 | 77 | |
| Total | 68 | 332 | 400 | |
Efter en körning av Crosstabs i SPSS får vi dels en tabell med våra värden. Från denna kan vi själva få en känsla för fördelningen mellan utbildningskategori och position på arbetsmarknaden. Det känns med sunda förnuftet att det är en klar påverkan där endast 2 personer av 77 som har högre utbildning är arbetslösa, medan 66 personer av 323 lågutbildade saknar arbete. I den här uppgiften använder jag bara SPSS beräkningar.
Chi-Square Tests | |||||
Value | df | Asymp. Sig. (2-sided) | Exact Sig. (2-sided) | Exact Sig. (1-sided) | |
| Pearson Chi-Square | 14,019a | 1 | ,000 |
|
|
| Continuity Correctionb | 12,783 | 1 | ,000 |
|
|
| Likelihood Ratio | 19,055 | 1 | ,000 |
|
|
| Fisher’s Exact Test |
|
|
| ,000 | ,000 |
| Linear-by-Linear Association | 13,983 | 1 | ,000 |
|
|
| N of Valid Cases | 400 |
|
|
|
|
| a. 0 cells (,0%) have expected count less than 5. The minimum expected count is 13,09. | |||||
| b. Computed only for a 2×2 table | |||||
Med SPSS analys av Chi2 ser vi (fortfarande på Pearsons värden) att vårt Chi2 är så högt som 14,019 och med samma antal frihetsgrader (1 st) som i förra exemplet passerar vi gränsvärdet med stor marginal. Att det utfall som vi observerar skulle vara slumpmässigt anges till 0,000 som är bättre än 0,1 % nivån%! Det kan vara lätt att lockas till en övertro på styrkan av analysen med ett utfall på 100 % sannolikhet för att det föreligger ett beroende. Vi skulle dock behöva arbeta mer med materialet för att studera just styrkan, vilket Chi2-testet inte ger något underlag till.
Slutsatsen är dock att det föreligger en signifikant skillnad vad gäller utbildningskategori (hög/låg utbildning) och position på arbetsmarknaden.
Djurfeldt Göran, Larsson Rolf, Stjärnhagen Ola (2003). Statistisk verktygslåda. Studentlitteratur
Betyg: 6 pooäng (av 6 möjliga) Hej! Tydligt och bra redovisat. Samtliga resultat är korrekta./Sven
Examination 4 – Datoruppgift 3
Regressionsanalys
Vi ska nu jobba med filen Dataövning3.sav som ni hittar på samma ställe som de övriga filerna.
För att utvärdera om kvinnor är diskriminerad på arbetsmarknaden, främst med avseende på lön, gentemot män kan man använda sig av tvärsnittsdata och genomföra en regressionsanalys. Vi har även tillgång till variabler som talar om etnisk bakgrund. Till en början kommer vi att genomföra en enkel linjär regression. Där vi endast tittar på kön som förklarande variabel, för att därefter utveckla modellen till att bli en multipel regression.
Den datamängd som vi ska jobba med är amerikans data från “Current Population Survey of the U.S. Bureau of Census”.
Följande variabler finns i datamängden:
- Lön, mätt i dollar per timme
- Kön 1=kvinna, 0=man
- Utb (=utbildning) mätt i antal år
- Ålder mätt i antal år
Uppgift 3.
Genomför deskriptiv (beskrivande) statistik över de variabler som vi har tillgång till.
(obs! tänk till vilka variabeltyper som ingår, dvs. nominal, ordinal, intervall eller
kvotdata och använd lämpliga centralmått och spridningsmått). Beskriv även med
ord hur den beskrivande statistiken ser ut.
Uppgift 4.
Genomför en enkel linjär regression med lön som beroende variable och utbildning som den oberoende variabeln. Tolka sedan resultatet ni erhåller. (Experimentera gärna med övriga variabler.)
Svar: (Ladda ner inlämnat dokument)
Uppgift 1
Deskripitiv statistik
Lön
Variabeln Lön är en kvotvariabel, även om vi knappast kommer att uppleva några negativa värden. Det är sannolikt vår intressantaste variabel i undersökningen, och mot vilken vi vill göra våra jämförelser och bivariata analyser.
Descriptive Statistics | ||||
N | Minimum | Maximum | Mean | |
| Lön | 206 | 3,0 | 25,0 | 9,60 |
| Valid N (listwise) | 206 |
|
|
|
Det aritmetiska medelvärdet enligt SPSS är $9,60. Med ett min på $3 och max på $25 ser vi direkt att det är en skev fördelning av lönerna och med en tyngdpunkt neråt. Det ger en intressant input till fortsatta analyser kring kopplingen mellan lön och de övriga variablerna. När vi beskriver lön univariat kan vi gå vidare och se på spridningen.
Statistics | ||
| Lön | ||
| N | Valid | 206 |
| Missing | 0 | |
| Median | 8,91 | |
| Percentiles | 25 | 5,50 |
| 50 | 8,91 | |
| 75 | 12,00 | |
Vi ser att medianen är $8,91 vilket till och med är lite lägre än medelvärdet, och att hälften av värdena ligger inom spannet $5,50 till $12.00. Den upplevda snedfördelningen kan undersökas vidare i ett histogram som visar spridningen på ett mer lättfattligt sätt.
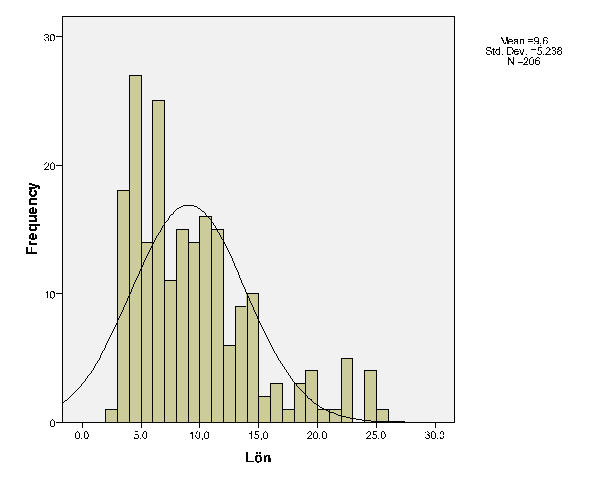
Histogrammet visar att fördelningen är förskjuten åt det lägre intervallet, upp till $15 och ett mindre antal löner ligger därutöver.
Med ett lådagram kan spridningen analyseras vidare.
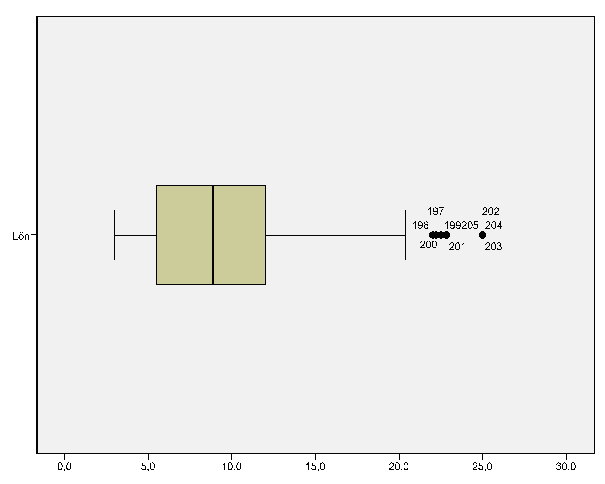
Vi har ett antal värden som enligt SPSS klassificeras som uteliggare. Det är de värden som är $22 eller över. De hamnar inom det spann mellan 1,5-3 lådbredder som identifierar uteliggare (Djurfeldt, 2003:63f). Lådbredden beräknas som Q3-Q1 och i exemplet med Lön är det $12,00 – $5,50 = $6,50. Det ger ett spann som sträcker sig från $12,00+1,5*$6,50=$21,75 till $12,00+3*$6,50=$31,50. Ovanför $31,50 kallas värdena extremvärden men några sådana har vi inte i vårt datamaterial.
Kön
Kön är en nominalskalevariabel med endast två värden. Det finns inget bra central- eller spridningsmått för nominalskalevarabler (Djurfeldt, 2003:49). Vi kan dock visa frekvensen för de två värdena för att få en bild av fördelningen.
Kön | |||
Frequency | Percent | ||
| Valid | Man | 105 | 51,0 |
| Kvinna | 101 | 49,0 | |
| Total | 206 | 100,0 | |
Den relativa fördelningen mellan Man och Kvinna är ganka jämn. Av de 206 mätningarna är 105 stycken män och 101 stycken kvinnor, vilket i relativ frekvens fördelar sig på 51% män och 49% kvinnor. Ytterligare användning av Kön kommer i analyser av de andra variablerna.
Utbildning
Utbildning mäts som totalt antal år som studerats. Det är en kvotskalevariabel även om vi inte ser några negativa värden.
Descriptive Statistics | |||||
N | Minimum | Maximum | Mean | Std. Deviation | |
| Utb | 206 | 2,0 | 18,0 | 13,2 | 2,6008 |
| Valid N (listwise) | 206 |
|
|
|
|
Vi har i undersökningen ett medelvärde på 13,2 års utbildning. Det känns rimligt med en grundskola på 8-10 år och några rs extra utbildning i allmänhet. Vi har ett riktigt extremvärde som min med endast 2 års utbildning. Det sticker ut jämfört med alla andra, och behöver undersökas närmre, eller kanske väljas bort i det fortsatta arbetet. Vårt maxvärde är 18 års utbildning och inte alls orimligt. Vi har många värden på både 16, 17 och 18 års utbildning vilket är logiskt med ett antal ytterligare år på college och universitet efter high scool. Vår standardavvikelse är 2,6 år och jag upplever det som lågt, vilket innebär en rätt tight spridning.
Statistics | ||
| Utb | ||
| N | Valid | 206 |
| Missing | 0 | |
| Median | 12,000 | |
| Percentiles | 25 | 12,000 |
| 50 | 12,000 | |
| 75 | 16,000 | |
Spridningen ser extra intressant ut när vi jämför median och percentiler enligt ovan. Medianen är samma som värdet på den 25-procentiga percentilen. Det beror sannolikt på väldigt många värden på just 12 års utbildning.
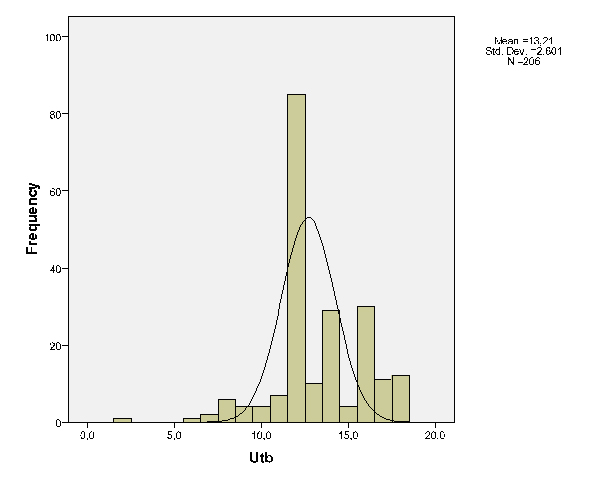
I ett histogram ser vi också tydligt att tre utbildningslängder är mest representerade; 12 år, 14 år och 16 år. Bortsett från vårt extrema minvärde på två år är övriga värden samlade.
Med ett lådagram ser vi ytterligare vikten av att analysera de enskilda mätvärdena innan vi fortsätter med korrelationer.
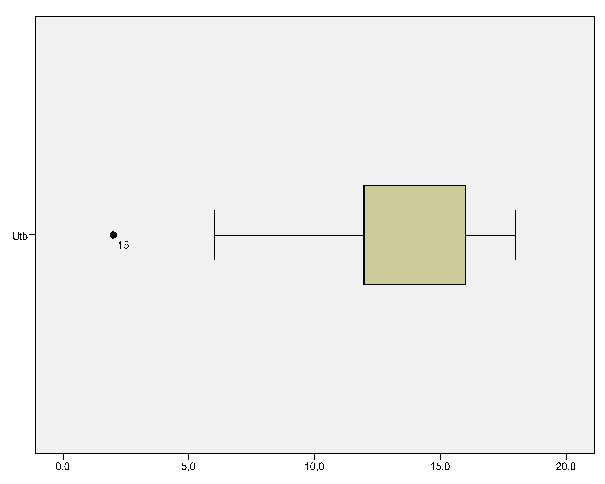
Det blir i lådagrammet extra tydligt hur vårt värde på 2 års utbildning är en uteliggare och att det sannolikt beror på felrapportering eller liknande.
Ålder
Ålder är likt Utbildning och Lön en kvotskalevariabel.
Descriptive Statistics | |||||
N | Minimum | Maximum | Mean | Std. Deviation | |
| Ålder | 206 | 18,0 | 64,0 | 37,112 | 11,8894 |
| Valid N (listwise) | 206 |
|
|
|
|
Medelvärdet för ålder är 37,1 år med min och max på 18 respektive 64 år. Medelvärdet ligger lite lägre än mittpunkten mellan max och min vilket ger en signal om en förskjutning neråt. Minvärdet känns rimligt med tanke på att den grundläggande utbildningen bör ha avslutats och personen börjat att arbeta. Maxvärdet är också rimligt, någonstans i nivå med en tänkt pensionsålder.
Statistics | ||
| Ålder | ||
| N | Valid | 206 |
| Missing | 0 | |
| Median | 35,000 | |
| Percentiles | 25 | 28,000 |
| 50 | 35,000 | |
| 75 | 44,000 | |
Medianen ligger på 35 år, ganska nära vårt medelvärde vilket är en signal på att vårt datamaterial känns välfördelat.
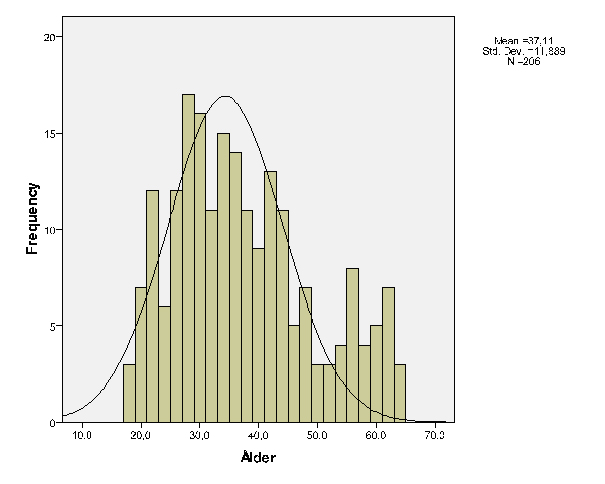
Histogrammet visar en mindre förskjutning neråt i ålder. Det är dock inga uteliggare eller extremvärden så åldersfördelningen känns väl fördelad.
Uppgift 2
Regressionsanalys
Om vi vill analysera sambandet mellan Lön och Utbildning genomför vi en regressionsanalys. Vi kan först titta på ett spridningsdiagram för att få en uppfattning om hur vårt datamaterial ser ut.
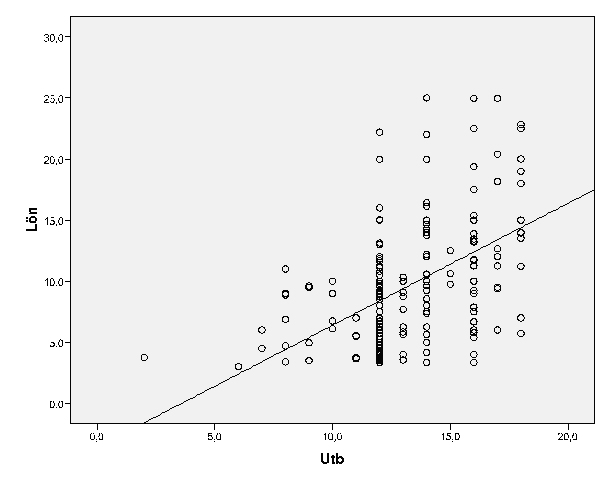
Vi ser med blotta ögat att de högre lönenivåerna återfinns hos dem med de längre utbildningarna. Däremot är spridningen av Lön för varje värde på Utbildning väldigt stor. Det existerar värden på minimiivå för nästan varje värde på utbildningslängd. En snabb första kommentar kan vara att för höga löner krävs en lång utbildning, men det är ingen garanti. Vi ska dock analysera vidare med de verktyg vi har till förfogande.
Det går att pröva samband på två olika sätt (Djurfeldt, 2003:278) nämligen variansanalys av regressionen samt ett test av lutningen av regressionslinjen (betakoefficienten b), och från vår körning i SPSS får vi material för att genomföra båda.
Test av betakoefficienten
Vi får material från SPSS som beskriver vårt sambands lutning. Formeln för regressionslinjen y = a + bx där y är vår beroende variabel Lön och x är vår oberoende variabel Utbildning och där b är betakoefficienten som visar lutningen på linjen. Linjens skärningspunkt för x = 0 representeras av a.
Coefficientsa | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
B | Std. Error | Beta | ||||
| 1 | (Constant) | -3,600 | 1,649 |
| -2,183 | ,030 |
| Utb | ,999 | ,122 | ,496 | 8,155 | ,000 | |
| a. Dependent Variable: Lön | ||||||
Vi kan avläsa betavärdet, dvs. linjens lutning, till 0,999 och signifikansen som representeras av t-värdet 8,155 till starkare än 1% nivån, ja till och med 0,1% nivån. Det innebär att vi i färre än ett försök av tusen skulle ha fått ett slumpmässigt resultat som gett denna linje. Om vi också häntar ner värdet a från materialet (i cellen för B och (Constant)), -3,6 så kan den slutliga formeln för vårt samband skrivas y = -3,6 + 1,0x.
Vi kan alltså konstatera att vi har ett samband och att dess lutning är -0,999 och signifikant till 0,1% nivån. Slutsatsen är att variationen i Lön är orsakad av Utbildning och att vår formel kan uttryckas som y = -3,6 + 1,0x.
Variansanalys av regressionen
Vi fortsätter med att studera variansanalysen av regressionen genom att beräkna prediktionsförmågan R2. R2 är den andel av den totala variationen i y som vi kan förklara med sambandet vi nyss beräknat ovan (Djurfeldt, 2003:168f).
Model Summary | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | ,496a | ,246 | ,242 | 4,5600 |
| a. Predictors: (Constant), Utb | ||||
Vid körningen i SPSS får vi två typer av införmation. Dels den uträknade koefficienten r som upphöjd till 2 ger vårt R2. I detta fall är R2=0,246 vilket betyder att 24,6% av den totala variationen i Lön kan förklaras med Utbildning.
ANOVAb | ||||||
| Model | Sum of Squares | Df | Mean Square | F | Sig. | |
| 1 | Regression | 1383,029 | 1 | 1383,029 | 66,512 | ,000a |
| Residual | 4241,937 | 204 | 20,794 |
|
| |
| Total | 5624,967 | 205 |
|
|
| |
| a. Predictors: (Constant), Utb | ||||||
| b. Dependent Variable: Lön | ||||||
Den andra typen av information vi fick efter körningen i SPSS ger oss värden på Regression, Residual och Total variation. Vi beräknar R2 genom formeln (Djurfeldt, 2003:171) Regressionen / Totala variationen, 1383,029/5624,967 = 0,246 och samma som i tabellen ovanför. Värdet på R2 känns ganska lågt. Den går mellan 0 till 1 och signalerar ett högt samband mellan x och y ju närmre 1 den når. Vårt beräknade värde på 0,246 får anses ganska lågt med tanke på att 0 innebär inget samband alls. Men signifikansen för detta värde (R2=0,246) är dock högt, uppe på och förbi 1% nivån. Därför blir slutsatsen att det visst finns ett signifikant samband mellan Lön och Utbildning men att vår prediktionsförmåga är ganska begränsad då endast 25% av variationerna i Lön kan förklaras med Utbildning.
Sammanfattning
De uteliggare vi observerat i tidigare analyser av variablerna är inte hanterade i regressionsanalysen ovan. En snabb kontroll i SPSS visar små effekter av utfallet och påverkar inte våra slutsatser. Vi kan definitivt påvisa ett samband mellan Lön och Utbildning även om det är svagt. Däremot kan vi inte med denna analys på något sätt konstatera att en hög lön kräver en lång utbildning och att en ännu högre lön kräver en ännu högre utbildning. Det är snarare så att det vårt datamaterial kan säga oss är att det krävs någon form av fortsatta studier för att nå de högre lönenivåerna, för det är efter 12 års studier som de högre lönerna dyker upp. I det dataspannet (12-18 års utbildning) är dock sambandet marginellt svagare än i det totala urvalet. Fortsatta studier behövs för att hitta fler och bättre samband, sannolikt med andra oberoende variabler.
Djurfeldt Göran, Larsson Rolf, Stjärnhagen Ola (2003). Statistisk verktygslåda. Studentlitteratur
Betyg: G
Examination 5
Denna del av examinationen är att skriva en promemoria (PM). Denna PM skall skrivas som en vetenskaplig rapport. Den skall behandla ett valt problemområde och en empirisk undersökning skall göras.. Det är fritt fram att välja problemområde med anknytning till sociologi och undersöka det, men insamling av data skall ske via enkäter (i boken- Från Datainsamling till Rapport – av Dahmström (2000) kan ni få tips om hur en enkätundersökning kan göras). Undersökningen kan göras vartsomhelst där ni kan få tag på respondenter (personer som fyller i enkäten) tex bland vänner, släktingar, studenter eller på jobbet. Det kan vara svårt att få tag i respondenter under denna korta tid som PM-arbetet gäller, men försök att få in minst 20 svar. Med färre svar blir det svårt att analysera materialet.
Syftet med rapporten är att ni skall lära er gången i forskningsprocessen, från ett problem, en frågeställning till färdig rapport med beskrivning och analys av problemområdet och de uppställda syftena. Rapporten skall vara skriven så att den sånär som uppfyller kraven för en vetenskaplig publikation och ska innehålla:
- Minst två hypotesprövningar, d.v.s. en hypotes som testas med lämplig statistisk metod
- Samtliga variabler som ingår i rapporten skall beskrivas med deskriptiv statistik
- Minst en variabel beskrivs grafiskt (tex stapel- eller histogram)
- Resultaten från analyserna ska redovisas i lämplig tabellform och ni ska kunna motivera all information i tabellerna. (Det brukar bli bäst om tabellerna görs i Excel el dyl. Det är dock ok att klistra in tabeller från SPSS).
Källor i rapporten skall skrivas ut enligt den praxis som Backman föreskriver i sin bok Rapporter och uppsatser.
Rapporten får vara mellan 2 000 – 3 500 ord (för att i Word kontrollera hur många ord ni skrivit, gå in i menyn “Verktyg”. Där finner ni “Räkna ord”).
Svar: Finns endast att ladda ner som inlämnat dokument :)
Betyg: 16 pooäng. Hej Peter! Din redovisning är bra och har en tydlig struktur. Det är lätt att följa med i Dina tankebanor, eller den röda tråden om man så vill. Din inledning och problembakgrund hade vunnit på en redovisning av faktisk arbetsfördelning av dessa uppgifter i svenska hem, det borde gå att få fram sådan statistik från SCB el dyl.
Att säga att Du har en ”stark hypotes” kan anses något överdrivet med tanke på att Du inte presenterar någon teoretisk grund för denna hypotes. Dessutom snubblar man lite på tungan/i tanken när man ska försöka förstå vad som menas med: ”fler som upplever att de fattar beslut än vad det är som upplever att någon annan fattar besluten”, det Du undersöker är ju skillnaden mellan mä/kvinnor i upplevelsen av just detta (vilket Du mycket riktigt skriviver i meningen efter). Vad gäller tillvägagångssättet att plocka bort alla ensamstående ur materialet torde det vara okej, men Då skulle Du även ha formulerat om syftet till att studien gällde när, vem, hur-städa i parförhållanden.
När man gör en studie är det naturligtvis forskaren själv som bestämmer om alla svar som samlats in ska analyseras och redovisas i samma rapport. De variabler som på något vis redovisas i rapporten ska dock vara av relevans för frågeställningen. Därför undrar jag varför Du i figur 1 redovisar ålder i gruppen.
Det Du hade kunnat göra var att lägga till en hypotes och köra en regressionsanalys med ålder och antal kr som spenderas på städmateriel. På så vis hade Du även fått med en regressionsanalys och det hade inte varit någon nackdel (något forcerat tillvägagångssätt om det varit verklig forskning kan tyckas, men nu handlar det ju mera om att redovisa förvärvade färdigheter). Det är synd att Du inte ställde frågan om hur ofta toaletterna städas öppet också, alltså i stil med: Hur ofta städar ni toaletterna per vecka hemma hos er”? Med öppna svarsalternativ som 1, 2, 3, 4, 5, ggr osv. hade Du ju kunnat göra en regressionsanalys på detta också.
Något som får anses vara en petig kommentar, men faktiskt inte desto mindre viktig, är att förklaringstexter till tabeller/figurer brukar placeras under desamma. Den deskriptiva statistiken i tabell 1-4 är något förvirrande men jag misstänker att ”Kön” slunkit med i rubriken av misstag. Vad gäller deskription i övrigt hade jag önskat en tabell för samtliga variabler som ingår i studien med central och spridningsmått. Detta har Du med under figur 1 ålder, men ingen annanstans. Det är som sagt ett bra arbete med flera kvaliteter, och, ett intressant ämne. Resultatet för rapporten blir 16 poäng vilket gör att Du kommer upp i betyget B för hela kursen.
Mvh
Sven
Underbart!
Men jag måste undra hur hinner du?
Jag skall med stort intresse ta del av dina anteckningar från i lördags.
lisa
Peter, du är ju sanslöst bra!!
Jag var själv på samma föreläsning men den här sammanfattningen var helt enkelt kanon! Tack!
Hej Lisa och Monica, tack för er fina återkoppling :) Det var en höjdare att ha med sig PC på föreläsningen och att använda universitetets fria trådlösa nätverk till att surfa på wikipedia samtidigt ;)
Jag hinner nog inte alls Lisa… Har bekymmer med alla mina prioriteringar men är väldigt stolt över att ha skickat in ett “slarv-exemplar” av tentan redan i lördags. Kanske inte så mycket slarv, men jag har tur om jag får godkänt tror jag ;) Vi får väl se…men jag prioriterade annat den gången!
Hej
Otroligt vad mycket du har hunnit få ner! Tack för det, mycket värdefullt för en som inte var där// Veronica
Hej Veronica, vet du vad? Efter att ha fått återkopplingen från Kattis i delkurs ett att jag skriver för mycket, så känner jag att jag hamnat i rätt vatten när det gäller anteckningsskrivande :) Det finns ingen gräns för hur mycket man (läs: jag) kan skriva när man slipper vetenskapliga stängsel ;)
Jag bävar för att läsa Backman :D
Men helt klart så går det att skriva för mycket och jag tror att du ibland skriver massiva mängder text för att dölja skamframkallande hål i kunskapen? Dina anteckningar är mycket men det saknas en tråd och en linje i resonemanget. Det kan tänkas att tillskrivningen för detta bör placeras hos din lärare, men yttermera visso har du ett ansvar för din vetenskapliga produktion, må det vara anteckningar eller så kallat råmaterial.
Dock finner jag viss behållning i dina reflektioner över de värdsliga situationerna på din webplats och jag tilltror dig stora möjligheter att kombinera dessa med en större dos sociologisk teori och korrekt språk.
Mig har du definitivt fått på kroken. Jag har läst det mesta av det du skrivit, nu på slutet också ditt socc-snack och blivit såld på kuppen :) Jag har sökt in till en sociologikurs för våren nästa år och ska försöka själv. Jag måste få chansen att förstå alla stackare som gör livet surt för mig så att jag kan få dom att fatta hur de måste skärpa till sig!
Tack för återkopplingen Fil.Dr. Nu har jag äntligen blivit klar med första uppgiften på vetenskaplig metod. Den är kortare och mer kärnfull än något jag skrivit tidigare…tror jag :) Ändå har jag fått med en del exempel ur det verkliga livet…
Men helt klart är att det är svårt…
Kul @nders K. att du ska gå sociologi. Var då?
Tack för bra anteckningar!
Jag har tenta på torsdag i sociologisk metod och har använt dina anteckningar och uppgifter som repetition nu i helgen, väldigt bra!
MVH
Carina
Tack för din kommentar! Alltid kul att få reda på om någon haft nytta av, eller fått sin dag förgylld av något här på webplatsen :) Hoppas att det går bra på tentan. Jag sitter med en om moderna klassiker som ska vara inne på söndag. Jag tyckte att metodavsnittet var lättare ;)
Tack så mycket för detta, har tenta på samhällvetenskapliga metoder den 12 november och detta kommer starkt att gynna mig!!
Tack SarA, kul att det hjälper, och lycka till :D